由于游戏的娱乐性和趣味性,时下玩游戏的人越来越多。除了娱乐以外,许多游戏中也蕴含着数学思想。例如经典的魔塔游戏中的路线选择问题背后就蕴含了图论的思想,红宝石转换塔背后更是蕴含着算法的思想。此外,兰切斯特方程一定程度上可以指导即时战略游戏中的决策,王者荣耀等游戏中可以通过伤害计算公式来度量装备的收益。你有哪些在游戏中应用数学思想的经历呢?一起来看看答主 @择梦舟的回答吧~
玩游戏时,你用过哪些数学思想来辅助你的决策?
| 答主:择梦舟
有的兄弟有的。
刷视频刷到过镜的「Z字抖动」,我就试着用几何语言描述落点位置。
镜的特点在于她的镜像,镜使用一技能或者二技能的时候,可以召唤一个镜像,这个镜像可以存在大约 2.3 秒钟
①镜像会镜像复制本体的动作,也就是本体做什么,镜像就会镜像地做什么;
②既然是镜像复制,就需要有一个类似镜面的线,一切镜像动作都是以这条线为基准的;
一技能会突进一段距离,距离大概是 400 码,也就是闪现的距离,其镜面线是突进的方向;
二技能虽然是原地释放,但有一个释法方向,在技能释放的时候可以看到,其施法方向就是镜面线的方向;
新版本的镜神增加换位的机制,即本体和镜像在 2.3 秒钟的存在时间内能实现换位。
于是,我们可以弄些骚操作,比如去年很火的 Z 字抖动。具体效果如下:
在训练营里开了无冷却(实际上镜的被动能刷新技能),第三次镜像最好开二技能,因为一技能会打断换位过程。
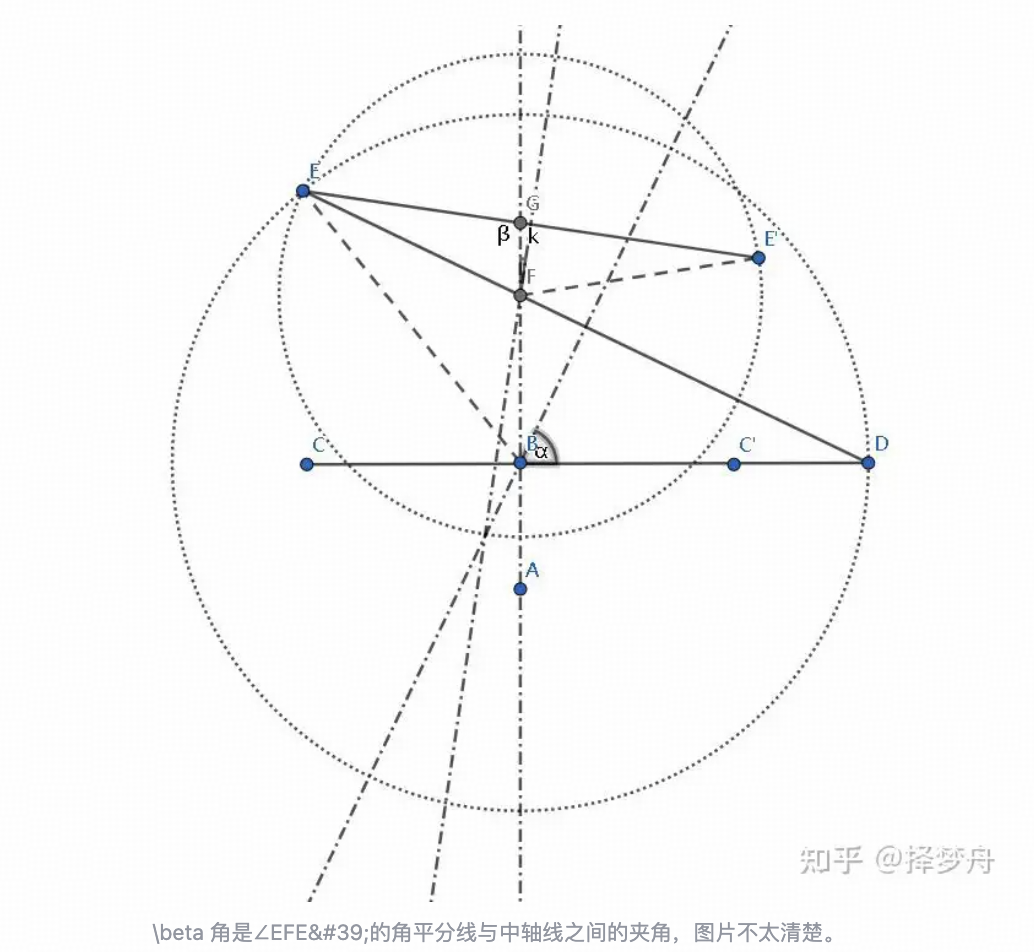
这里用理想情况下的简化图讲解一下具体过程:
镜在 A 点,一技能突击到 B 点,产生镜像走到 C 点,等到镜像即将结束时换位,到 B 点时用二技能产生新的镜像,换位到 D 点等到镜像即将结束时,换位(此时头顶能量条也快结束),到 F 点时用二技能产生新的镜像,换位到 E 点,换位,到 G 点时用一技能或三技能攻击对手。
初始点(镜): A
终点(对手): G
本体(实线部分): 换位换位A⇒B⇒C⇔C′(换位)⇒D⇔E(换位)⇔G
第一次镜像的产生: A⇒B (一技能)
第二次镜像的产生:在 C⇔C′ 换位过程中经过 B (二技能)
第三次镜像的产生:在 D⇔E 换位过程中经过 F (二技能)
这里有个问题,就是产生第二次镜像时很难根据 G 点位置确定二技能的施法方向,这里进行讨论
我们已知镜的基础移速是 385 码/秒,而闪现距离为 400 码,镜像产生时间为 2.3 秒(一般我们 2 秒换位一次),一技能突进距离为一个闪现距离。
记第二次产生镜像时二技能施法方向为 α ,闪现距离为 l , C′D=d ,

当然实战时候,可能由于敌人走动或者紧张导致第三次产生镜像的施法角度发生偏差,不会形成标准的 Z 字。

既然理论已经算出来了,那可以实操了。